The current forecasts gives us a 50/50 chance of catching this event in Austin. If you plan to photograph this event now is a good time to make plans. This is walk through my planning to pick a lens for a fixed tripod shot. I want to capture the eclipse from Austin, Texas from the start of the partial eclipse to near maximum eclipse at sunrise.

One of the first things I consider in planning an astrophotography shot is the field of view that I will need to capture. This tells me the lens or telescope that I will need to capture the portion of sky that I need to.

If it’s a conjunction that I’m shooting I’ll go to my preferred planetarium program (SkySafari) and measure the separation of the two planets as viewed from my shooting location.

For this lunar eclipse, I want to capture the eclipse from the start of the partial eclipse at 5:48 AM CST until sunrise at 7:22 AM from a camera on a fixed tripod. This is 1 hour and 34 minutes or 1.57 hours. Because the Moon is relatively near the celestial equator, I can quickly calculate the field of view required with a little geometry and timing.

a geometric approach

The sky appears to rotate 360 degrees in 23.56 minutes, just about 15 degrees/hour. The Moon moves the same direction as the earth's rotation (360 degrees in 27.3 days or about 0.5 degrees, the width of the full Moon, in an hour. This is in the opposite direction from the sky's apparent motion. Thus I expect the Moon to move 1.57 x (15 - 0.5) or about 23 degrees during the time I want to shoot the eclipse.

We can calculate the formula for the needed focal length lens from

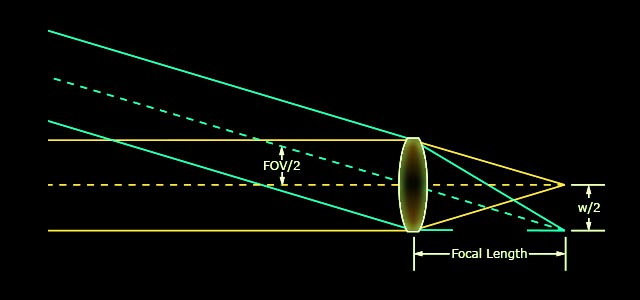
FOV/2 = arctan (w/2f)
tan(FOV/2) = w/2f
f = w / (2 * tan(FOV/2)
where f is the focal length in mm, w is the camera sensor width in the same units , and FOV is the field of view required.

For my eclipse shot and a 1" sensor camera
f = 13.2 mm / 2* tan(23/2) = 13.2 / 0.407 = 32.4 mm

for an APS-C camera
f = 23.5 mm / 0.407 = 57.7 mm

for a full frame camera
f = 36 mm / 0.407 = 88.5 mm

We should also allow a border in our shots. The calculations above use the long sensor distance, but the shot will have the Moon moving diagonally across the frame. A 3:2 aspect ration frame has a diagonal that is about 20% greater than the long side. A full frame focal length of 90mm is the maximum focal length that I could expect use for this shot. 70mm should allow for more relaxed framing.

small FOV approximation

I can't calculate tangents in my head, so I like to use the small angle approximation. The tangent of a small angle is equal to the angle's value in radians (1 radian = 180/pi = 57.3 deg.). Using this we can simplify our formula to:

f = w * 57/FOVwith FOV in degrees

Is 23 degrees a small angle? Let's check the full frame case:
f = 36mm 57/23 = 89.2 mm
which is a focal length less than 1mm different from the exact calculation!

the easy way with a planetarium app

A planetarium program like SkySafari will most of this work for you. I use a reticle that corresponds to my camera sensor and lens or telescope positioned on my target in the sky map.

For my 1" sensor camera I chose a 25.7 mm (2.7x crop factor, 70mm FF equiv.) lens. For my APS-C camera, my nearest lens size is 60mm (1.5x crop factor, 90mm FF equiv.) , which frames the shot very tightly. I've layered SkySafari screen shots from the start of the partial eclipse until sunrise in the image below:

tips

• If your planetarium application supports telescope specific FOV cursor reticles like SkySafari, you can enter your camera lenses just like a telescope. Some lenses are marked with full frame equivalent focal lengths, be sure to use the native focal length instead (FF_fl / crop_factor).
• When your planetarium app doesn't support custom camera or telescope cursor reticles, it may have a circular reticle that you can customize to a specific field of view. Just use FOV= 2 arctan (w/2f) to calculate the FOV for your sensor size and focal length and use this as the reticle size.

Here is how the shot actually turned out!