Estimating image resolution by re-sampling

How can you estimate the resolution of an image with no obvious resolution target? On targets like the Moon with permanent surface features, this is relatively straightforward. Find the smallest feature that is resolved (e.g. a crater). In images of planets with changeable surface features and less contrast this is more difficult to do. We can use re-sampling of the image to a test resolution as a way to estimate resolution.

Two ways of defining resolution

First let's look at two common ways of referring to resolution that are often confused. Optical measures of resolution are based on minimum resolvable separation of elements like lines or points. Something like the ISO 12233 test chart can be used. Astronomers use a similar measure based on the separation of closely spaced stars. The Rayleigh Criterion and Dawes Limit are based on this measure.

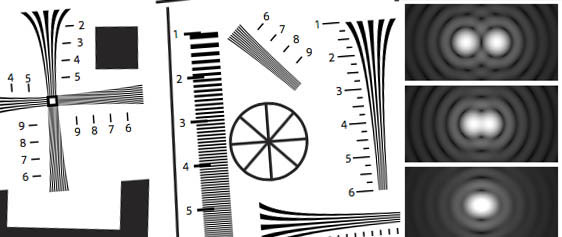
When working with digital images the size of an individual sample - a sensor element or a pixel in an image is often described as its resolution. This pixel size of the image may be different than the actual resolution of the original image. If the original image resolution was better than that of the sensor, that detail has been lost. We call this under sampling of the image. If the original image resolution was less than that captured by the sensor, no detail has been lost. This is called over sampling.

How are these ways of measuring resolution related: the smallest detectable separation between two points and how finely must the image be sampled and not loose detail? The Nyquist-Shannon sampling theorem describes the relationship between these two measures. A signal must be sampled at twice the rate of its fastest frequency (line spacing) to capture all of the detail (information) in the original image. An intuitive restatement: in order to distinguish two closely spaced points we must sample both the points and the space between them. Measurements made using the these definitions will differ by a factor of two. If you are digitizing an image with a line or point separation based resolution of 2 arc seconds, the size of the sampled pixels must be half this, 1 arc second.

It is common practice to use the line frequency based definition when talking about telescopes and the sample pitch (pixel) definition with digital images. It is easy to confuse the two, but they are different a factor of two!

Estimating real image resolution

When an image resolution has been over sampled, we can use the sampling theorem to estimate the real resolution of the image. We can down-sample the image to correspond to a lower resolution and see if we loose any detail in the image. If the down-sampled image has lost information, we know by the sampling theorem that the original image resolution was greater than that of the down-sampled image. In order to make a visual comparison of the down sampled image to the original image easy, up-sample the image back to match the sampling of the original image. If the re-sampled image shows the same details as the original image, then we know that the down sampled image resolution is better than the real resolution of the original image. By comparing images down sampled to a range of resolutions to the original, we can estimate the actual resolution of the original image.

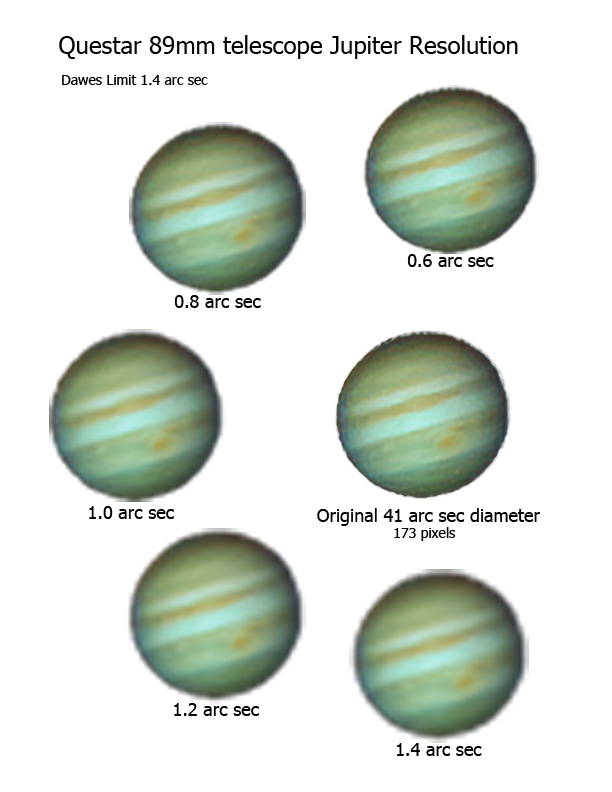
This is all much clearer in an illustration. The figure below shows a processed image of Jupiter in the center and versions of the image that have been re-sampled to pixel sizes that correspond to from 0.6 to 1.4 arc sec per pixel. Each of these was then up sampled back to match the original image in size. The 0.8 and 0.6 arc sec pixel images are closest to the original. Averaging these and applying our factor of two (sampling to separation) we estimate the original image resolution to be about 1.4 arc sec.

Comparing re-sampled image to detect processing artifacts

When we process images to sharpen them, mistaking artifacts for real image features is a concern. We can use a similar technique to validate a processing work flow, by comparing the processed image with a high resolution image that has been down-sampled to the same resolution. The example below compares of my images compared to one of Christopher Go's amazingly detailed Jupiter images taken a few days before. Christopher's image has been re-sampled to approximately the same resolution as mine.